Marge d'erreur (Sondage)
Introduction : Qu’est-ce que la marge d’erreur ?
La marge d'erreur est une mesure statistique qui permet de quantifier l'incertitude inhérente à un sondage ou à une estimation basée sur un échantillon, lui-même déterminé à. partir d'un groupe cible initial appelé population.
Elle permet d'indiquer dans quelle mesure les résultats d'un sondage sont à même de refléter l'opinion de la population globale étudiée.
La marge d'erreur est généralement exprimée sous forme d'un intervalle de confiance, qui donne une estimation du pourcentage ou de la moyenne réelle ainsi que de la probabilité d'erreur associée. Par exemple, si un sondage montre que 60% des personnes interrogées ont une certaine opinion, avec une marge d'erreur de plus ou moins 3%, cela signifie que la proportion réelle dans la population totale se situe probablement entre 57% et 63%.
La marge d'erreur dépend de plusieurs facteurs, tels que la taille de l'échantillon, le niveau de confiance choisi et la variabilité des réponses obtenues. Il est important de noter que la marge d'erreur ne mesure pas la précision absolue de l'estimation, mais plutôt l'incertitude statistique qui lui est associée. Ainsi, une marge d'erreur plus étroite indique une estimation plus précise, tandis qu'une marge d'erreur plus large indique une estimation moins précise.
Comment calculer la marge d'erreur ?
La formule pour calculer la marge d'erreur associé à la réalisation d'un sondage réalisé implique de connaître trois variables :
- la taille de votre échantillon - c'est-à-dire le nombre de personnes interrogées sur la base de votre population initiale(n),
- l'écart-type de la population (σ),
- le z-score (z)
La marge d'erreur reflétant le degré de certitude que l'on peut associé au résultat d'un sondage implique, en règle générale, d'avoir une valeur associée à cette marge comprise entre 1 et 10% (et il est déconseillé de dépasser ce seuil de 1%), avec une valeur commune associée de l'ordre de 5%.
Calculer l'écart type d'une population
L'écart-type est une mesure statistique qui permet de décrire la dispersion des données autour de la moyenne d'une population, et donc de déterminer si le profil de la population est centré :
- Étape 1 : Premièrement, il est nécessaire de calculer la moyenne arithmétique de la population (μ) en additionnant toutes les valeurs de la population et en les divisant par le nombre total de données.
- Étape 2 : pour chaque valeur estimée de la population, il faut soustraire la moyenne et élever au carré le résultat obtenu. Ces carrés des écarts par rapport à la moyenne doivent ensuite être additionnés.
- Étape 3 : il faut diviser enfin la somme obtenue par le nombre total de données de la population et prendre la racine carrée du résultat.
L'écart-type est exprimé dans la même unité que les données d'origine, ce qui permet de mieux appréhender la dispersion des valeurs autour de la moyenne.
L'écart-type est une mesure importante en statistiques car il permet de quantifier la variabilité des données et d'apporter une indication sur la précision des résultats obtenus. Ainsi, plus l'écart-type est élevé, plus les données sont dispersées autour de la moyenne et moins la mesure est précise. Au contraire, un faible écart-type indique une dispersion réduite et donc une plus grande précision des résultats.
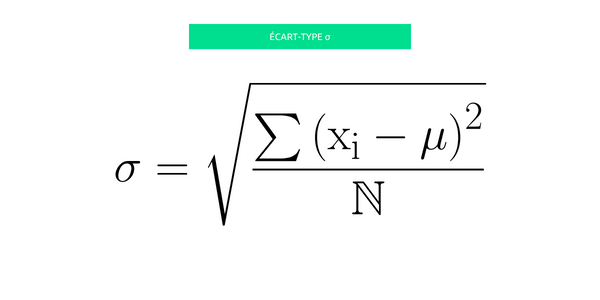
Calculer le z-score
Le z-score représente le nombre d'écarts types par rapport à la moyenne d'un point d'information. en d'autrs termes, il s’agit de la proportion du nombre d’écarts-types en dessous ou au-dessus de la population que représente un score brut.
Le z-score est calculé en soustrayant la moyenne (μ) de l'observation donnée (X), puis en divisant ce résultat par l'écart-type des données (σ).
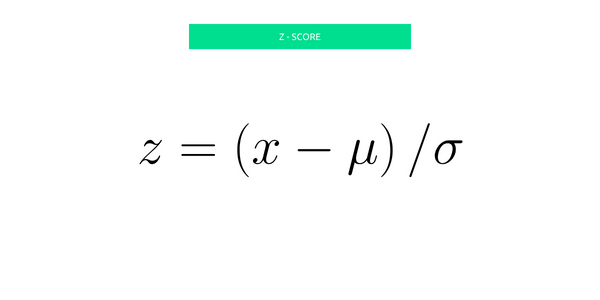
Plus le z-score d'une observation est élevé, plus elle est éloignée de la moyenne des données. Il est également possible d'utiliser le z-score pour déterminer le degré de confiance avec lequel une observation est éloignée de la moyenne. C'est d'ailleurs en ce sens que le z-score est utilisé dans le calcul de la marge d'erreur associé à un sondage client.
Par exemple, un z-score de 1,96 indique que l'observation se situe à environ deux écart-types de la moyenne, avec un degré de confiance de 95%. Un z-score de 2,58 indiquerait un degré de confiance de 99%.
C'est donc une mesure statistique importante pour évaluer la distance d'une observation à la moyenne et déterminer son degré de confiance, mais il est important de noter que le z-score n'est utile que si les données suivent une distribution normale. Si les données ne suivent pas une distribution normale, d'autres méthodes statistiques peuvent être nécessaires pour évaluer la distance et le degré de confiance d'une observation par rapport à la moyenne des données.
Pour simplifier le travail, voici un tableau représentant les z-score en fonction du degré de confiance souhaité (note: on privilégiera le plus souvent un intervalle de confiance de 95).
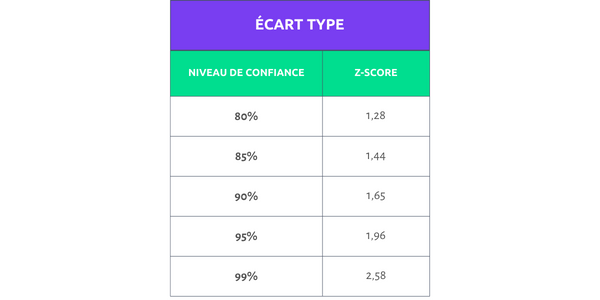
Calculer la marge d'erreur
L'écart-type et le z-score obtenu, nous pouvons enfin calculer la marge d'erreur.
Pour rappel, la marge d'erreur d'un sondage ne reflète pas le degré de véracité associé aux résultats mais permet de quantifier l'incertitude associée à une estimation statistique. En d'autres termes, la marge d'erreur indique à quel point les résultats d'une étude peuvent différer de la réalité.
Plus la taille de l'échantillon sera grande, plus la marge d'erreur sera faible, car les estimations statistiques seront plus précises.
Pour le calcul, la marge d'erreur (M) s'obtient en :
- Divisant l'écart-type (σ) par la racine carrée de la taille de l'échantillon (n),
- puis en multipliant le résultat par le z-score (z)
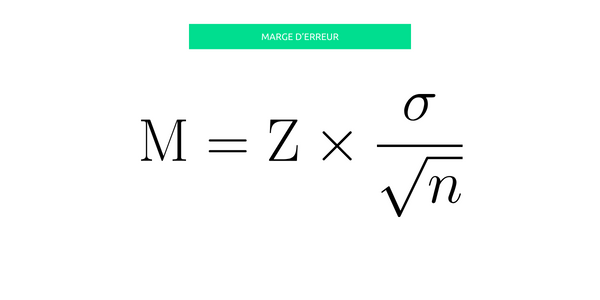
Support
Quel est l'impact de la marge d'erreur sur la taille de l'échantillon ?
La marge d'erreur joue un rôle crucial dans la détermination de la taille de l'échantillon, car elle est étroitement liée au degré de confiance souhaité dans les résultats. En effet, la marge d'erreur mesure l'ampleur des fluctuations statistiques possibles dans l'échantillon par rapport à la population totale.
Ainsi, plus la marge d'erreur est acceptable, plus la taille de l'échantillon peut être réduite. Cependant, il est important de noter que la marge d'erreur ne peut pas être complètement éliminée, car elle est inhérente à tout processus d'échantillonnage.
Pour diminuer la marge d'erreur, il est nécessaire d'augmenter la taille de l'échantillon, ce qui permet de réduire les variations aléatoires et d'obtenir des estimations plus précises des caractéristiques de la population étudiée.
Par exemple, si un degré de confiance de 95% est jugé acceptable, la marge d'erreur correspondante peut être fixée à ± 3%. Cela signifie que si la taille de l'échantillon est suffisamment importante, les résultats obtenus auront 95% de chances de se situer dans une fourchette de ± 3% par rapport à la population totale. En revanche, si la marge d'erreur acceptable est de ± 1%, un niveau de confiance souhaité plus élevé est nécessaire, ce qui entraîne alors une augmentation de la taille de l'échantillon afin d'obtenir des résultats fiables.
Par conséquent, l'impact de la marge d'erreur sur la taille de l'échantillon est directement lié au degré de confiance souhaité et à la précision désirée des résultats. Une réflexion attentive sur ces paramètres permet de déterminer la taille optimale de l'échantillon pour garantir des conclusions valables et représentatives de la taille de la population étudiée.
Les conséquences d'une marge d'erreur élevée dans un sondage
Une marge d'erreur élevée dans un sondage peut avoir différentes conséquences.
Tout d'abord, elle remet en question la fiabilité des résultats obtenus. En effet, si la marge d'erreur est élevée, cela signifie que les estimations peuvent être très éloignées de la réalité. Les décisions prises sur la base de ces résultats risquent donc d'être erronées. L'impact peut aussi se jouer en termes de crédibilité: les clients interrogées peuvent douter de la compétence et de la rigueur de l'équipe en charge de l'étude. Enfin, un autre effet indésirable d'une marge d'erreur élevée est qu'elle peut influencer le comportement des répondants. En sachant que leurs réponses peuvent varier considérablement, les personnes interrogées peuvent être moins enclines à donner des réponses sincères ou précises. Cela peut entraîner un biais dans les résultats et fausser l'interprétation des données.
Les différentes sources d'erreurs dans un sondage
Un sondage est un outil précieux pour recueillir l'opinion et les préférences d'un groupe de personnes. Cependant, il est important de reconnaître que les sondages peuvent comporter différentes sources d'erreurs. Tout d'abord, il y a l'erreur d'échantillonnage. Si l'échantillon de personnes interrogées n'est pas représentatif de la population cible, les résultats du sondage ne seront pas généralisables. Par exemple, si un sondage sur les préférences politiques est réalisé auprès d'un groupe uniquement composé de personnes âgées, il ne donnera pas un aperçu complet des opinions de la population dans son ensemble.
Ensuite, il y a l'erreur de non-réponse. Certaines personnes peuvent décider de ne pas participer à un sondage, ce qui peut biaiser les résultats. Par exemple, si les personnes qui sont peu satisfaites d'un produit sont plus enclines à ne pas répondre à un sondage de satisfaction, les résultats seront faussés en faveur du produit. De plus, il y a l'erreur de formulation des questions. Si les questions posées dans un sondage sont ambiguës, mal formulées ou orientées, elles peuvent influencer les réponses des participants et conduire à des résultats peu fiables.
Enfin, il y a l'erreur de l'intervieweur. L'attitude, le ton de voix ou les préjugés de l'intervieweur peuvent inconsciemment influencer les réponses des participants. Il est donc essentiel de former les intervieweurs à être neutres et impartiaux lors de la collecte des données.
Comment minimiser l'erreur de sondage pour obtenir des résultats fiables
Pour obtenir des résultats fiables dans un sondage, il est essentiel de minimiser les erreurs possibles.
Tout d'abord, il est nécessaire de veiller à ce que l'échantillon soit représentatif de la population étudiée. Pour cela, il convient de sélectionner les participants de manière aléatoire, en évitant tout biais de sélection. De plus, il est important d'utiliser des méthodes de collecte de données appropriées.
Les questions posées doivent être claires, sans ambiguïté et sans biais, afin de garantir des réponses précises et authentiques. Il est également crucial d'éviter l'influence du sondage sur les participants. Il est recommandé de garder les questions neutres et d'adopter une approche neutre dans le processus de collecte des données.
Il est tout aussi important d'obtenir un taux de réponse élevé, car un faible taux de réponse peut entraîner un biais dans les résultats. Pour cela, il est possible d'utiliser des incitations pour encourager la participation des personnes sondées.
Enfin, il est essentiel d'appliquer un traitement et une analyse statistique rigoureuse des données collectées via les résultats de vos sondages, afin de garantir des résultats fiables. En éliminant les erreurs potentielles dans toutes les étapes du processus de sondage, il devient possible d'obtenir des résultats précis et fiables.
Auteur:

Sébastien Neveu
Head Marketing
* NPS est une marque déposée et Net Promoter System est une marque de service appartenant à Bain & Company, Inc., Satmetrix Systems, Inc. et Fred Reichheld.
Blog
Continuez votre lecture avec les articles de notre blog sur le sujet.

Qu'est-ce qu'un bon score NPS ?

Les 6 limites du NPS

Comment réagir face à un NPS en baisse ?

Pourquoi catégoriser vos clients avec la segmentation NPS ?

Calcul du NPS : Comment calculer son Net Promoter Score ?
